Comment améliorer la disponibilité d’un système?
Quelques définitions
Soit un système S dont le fonctionnement est le suivant
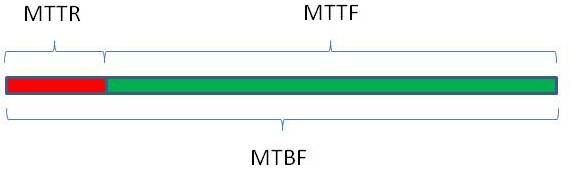
Au bout d’une période d’observation on peut en déduire des durées moyennes de marche et de pannes (jusqu’à fin de la réparation), d’où il vient le schéma suivant :
Où :
MTTR (Mean Time To Repair) est le temps moyen de panne jusqu’à la fin de la réparation)
MTTF (Mean Time To Failure) est le temps moyen consécutif de bon fonctionnement. Plus ce nombre est grand, plus le système observé sera fiable. L’inverse du MTTF est le taux de défaillance (nombre de pannes par unité de temps) classiquement représenté par la lettre grecque λ= 1/MTTF, il est exprimé en nombre de pannes par heure (h-1)
MTBF (Mean Time Between Failure) est le temps moyen entre déclenchement de pannes. Lorsque le MTTR est petit devant le MTTF, ce qui est le cas dans les systèmes que nous surveillons, on peut confondre MTTF et MTBF.
La disponibilité des systèmes est mesurée par le rapport entre le temps de bon fonctionnement et le temps total soit MTTF/(MTTR+MTTF) L’indisponibilité est le complément à 1 de la disponibilité soit MTTR/(MTTR+MTTF) qui en première approximation est égal à MTTR/MTTF.
Pour diminuer l’indisponibilité
Il est donc possible de jouer sur :
- La fiabilité de l’élément,
Augmenter cette fiabilité peut s’effectuer
-
- en changeant l’élément pas un élément jouant un rôle équivalent mais plus fiable (exemple remplacer une liaison CPL par une fibre Rose)
- en effectuant, si cela est possible, de la maintenance préventive. (entretien régulier, suivi des accroissements de taux d’anomalies, etc..)
- Le MTTR (temps moyen de réparation de l’élément),
Diminuer ce temps moyen de réparation peut s’effectuer
-
- En surveillant l’élément concerné pour déclencher le processus de réparation au plus tôt.
- En optimisant le MTTR.
- On peut jouer, à la marge, sur le temps de la réparation, par augmentation des compétences, par une meilleure capitalisation, par une organisation avec processus d’escalades efficient.
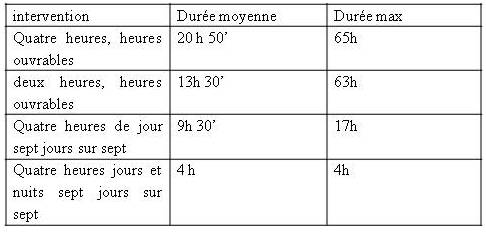
- Par raccourcissement du temps moyen d’intervention. Pour l’illustrer, prenons quatre exemples
Il est aisé de constater que la période de couverture du service joue un rôle plus important que le délai d’intervention, tant sur la moyenne, que sur les durées maximales possibles des pannes.
- La structure
On peut en effet multiplier les éléments en parallèle pour gagner en disponibilité.
-
- Le doublement
C’est une action largement répandue quel que soit le domaine (protection de secours, doublement des voies de communication, doublement des calculateurs de systèmes de commande, et plus simplement roue de secours des voitures)
En théorie, la mise en parallèle de deux systèmes réparables et surveillés, a un taux d’indisponibilité égal au produit des taux d’indisponibilité des éléments en parallèle. Ainsi, si un système a une centaine d’heures de pannes par an cela donne un taux d’indisponibilité de 1% (dispo 99%). Un système doublé aura donc une indisponibilité de 0,01% (dispo 99,99%) soit une heure de panne, en moyenne, tous les ans !
-
- Les limites rencontrées dans la pratique
Emporté par un élan mathématique, on pourrait envisager de tripler les éléments. Dans le cas précédent, on arriverait à une disponibilité de 99,9999% par an (moins d’une minute de panne en moyenne par an). C’est trop beau : Où est l’arnaque ?
-
-
- Les modes communs
-
« L’arnaque » n’est pas dans l’approche mathématique, qui est rigoureuse, mais dans les hypothèses (plus ou moins implicites) de départ. L’approche mathématique sous entend une indépendance totale des événements entre les deux éléments. Hors il n’en est rien. Le cas le plus fréquent est celui où les éléments sont issus d’un même fournisseur (mode commun de pannes). Ils peuvent s’appuyer sur des socles logiciels communs (ex ; Windows ou Unix) non nécessairement exempts de bugs. Ils peuvent avoir été paramétrés ou réglés selon un même modèle, éventuellement incorrect. Ils sont soumis aux mêmes environnements : alimentation électrique, climatisation, climat, fourreaux…).
-
-
- Les limites des modes multiples
-
Enfin, dans certain processus, une logique de choix entre les éléments concourant à la fonction est nécessaire, et, cette logique, est, en général difficile à spécifier, à construire et à tester. Elle possède, si elle a été réalisée avec soin, un taux de défaillance que je situe, au vu de mon expérience, comme étant de l’ordre de grandeur de celui d’un système doublé. (Ce qui rend généralement fictif le gain de disponibilité que l’on pourrait avoir à tripler les éléments).
-
-
- Les limites de la perfection intellectuelle…
-
L’expérience montre que lorsqu’un dysfonctionnement non nécessairement majeur apparait, l’ingénieur va chercher une solution pour le résoudre. Or, notamment dans les cas de redondance à chaud, les solutions apportées peuvent avoir un degré de complexité important rendant leur réalisation délicate et leur testabilité improbable. Par ailleurs dans les systèmes maillés présentant un niveau de complexité important, des effets de bord non prévus peuvent apparaitre. On voit donc émerger des solutions qui éliminent un certain nombre de défauts gênants mais non critiques et qui génèrent, de façon exceptionnelle –heureusement – des situations critiques dont la sortie peut être longue et laborieuse.
On peut d’ailleurs, sur ce point, faire un parallèle avec les réseaux électriques, pour lesquels les bouclages améliorent la qualité au quotidien, mais pourraient contribuer à l’apparition, dans des cas heureusement exceptionnels, de défauts non maîtrisables et d’incidents importants voire généralisés.